重水素の原子( 2H)は、
１つの電子、１つの陽子、１つの中性子からなっており、
電子スピンは1/2、核スピンは1になる。
反対の符号を持つスピン同志が対になると、
スピンとしての性質が見かけ上打ち消される。ヘリウムはその１例である。
MRIでは対になっていない核スピンが重要になる。
によって以下の式で決まる周波数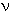 
の光子(photon)を吸収する。
= 
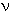B 
この核スピンを持つ同位体の存在比がNMR信号を検出するに足るだけ高いものだけがMRIの対象となる。MRI
の対象になる核のいくつかを以下に列挙する。
| Nuclei | Unpaired Protons | Unpaired Neutrons | Net Spin | (MHz/T)
|
|---|---|---|---|---|
| 1H | 1 | 0 | 1/2 | 42.58 |
| 2H | 1 | 1 | 1 | 6.54 |
| 31P | 0 | 1 | 1/2 | 17.25 |
| 23Na | 0 | 1 | 3/2 | 11.27 |
| 14N | 1 | 1 | 1 | 3.08 |
| 13C | 0 | 1 | 1/2 | 10.71 |
| 19F | 0 | 1 | 1/2 | 40.08 |
陽子は、スピンと呼ばれる特性を持っている。この特性はプロトンをN極とS極を持つ小さな磁石のようにふるまわせる磁気モーメントと考えることができる。
陽子が外部磁場の中に置かれたとき、磁石と同じように粒子は外部磁場の方向へ整列する。
N-S-N-Sのように整列した状態ではエネルギーの低い状態となり、N-N-S-S では高い状態になる。
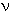とPlank定数(h = 6.626x10-34 J s)と関連している。
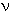
NMRおよびMRIでは、
は共鳴周波数またはラーモア周波数(Larmor frequency)と呼ばれる。
既に見たように 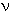= B ならびに E = h なので、2つの状態の間を遷移させるために必要な光子のエネルギーは
B
となる。2つのスピンの状態のエネルギー差と光子のエネルギーが一致する時、エネルギーの吸収が起こる。
NMRの実験では、光子の周波数はラジオ波(radio frequency,
RF)の帯域に相当する。NMRスペクロトスコピーでは水素原子核の場合、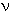は60〜800MHzになる。臨床用の水素のMRIでは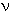は15〜80MHzになる。
もう一つの方法は、一定の磁場中で周波数を変える方法である。一定の磁場の大きさはエネルギー準位図のなかで垂直方向の青い線で表されている。
室温では低いエネルギー準位のスピンの数 N+が、高いエネルギー準位のスピンの数 N-よりもほんの少しだけ多くなる。ボルツマン統計によれば
Eはスピン状態間のエネルギー差、kはボルツマン定数で1.3805x10-23 J/Kelvin であり、TはKelvin単位の温度である。
温度が下がるに従って N-/N+の値は減少し、温度が増加するに従いこの比N-/N+は1に近づく。
NMRスペクトロスコピーの信号は、各状態の占有数の差に比例する。NMRはとても鋭敏なので、非常にわずかな占有数の差を検出することが出来る。これは共鳴現象、すなわち特定の周波数のエネルギーのスピンとスペクトロメータの間でのエネルギー交換によるものである。
各スピンパケット内のスピンによりつくられる磁場は、磁化ベクトルにより表すことができる。
それぞれのベクトルの大きさは(N+ - N-)に比例する。
スピンパケット内の全ての磁化ベクトルの和が巨視的磁化(net
magnetization)となる。以後，パルスNMRの話をするときは、磁化といえばこの巨視的磁化である。
NMRでの一般的な座標系では、外部磁場はZ軸に平行で、磁化もZ軸に沿ったものとなる。
2つのスピン状態間のエネルギー差に等しい周波数のエネルギーを核スピン系に与えると，磁化を変化させることが出来る。特に，十分なエネルギーを与えるとスピン系を飽和させて
MZ=0とすることができる。
MZがどのように平衡状態に戻るかをあらわす時定数をスピン−格子緩和時間(T1)と呼ぶ。このふるまいを支配する式は、変化を与えてからの時間をtとした場合
従って，T1は磁化のZ成分が(1-1/e)まで増加する時間として定義される。
磁化を-Z方向に向けると、T1に従って+Z方向の平衡状態に次第に近付いていく。このときのスピンのふるまいは変化を与えてからの時間をtとすると、以下の式で記述される。
スピン緩和時間(T1)は、縦磁化(MZ)と平衡磁化との間の差が1/eになるのに要する時間であるともいえる。
磁化がXY平面にエネルギー準位間の遷移を起こす光子の周波数に等しい周波数でZ軸の周りを回転し始める（＝歳差運動）。
この周波数をラーモア(Larmor)周波数という。
訳注：dephase = スピンパケットを構成する個々のベクトルの位相が乱れてゆき，このため巨視的磁化(net magnetization)が減少してゆく現象。いったんdephaseしたスピンの位相をなんらかの方法で再び揃えることをrephaseという。
この横磁化MXYのふるまいを記述する時定数はスピン−スピン緩和時間T2と呼ばれる。
T2 は常に T1よりも小さくなる。
平面内の磁化は0になりその後、縦磁化がZ軸の向きにMoの大きさになるまで回復する。
横磁化はどれも同じようにふるまう。
横成分は与えられた磁化のまわりに回転しながらdephaseする。T1は縦磁化の回復の率を表わしている。
以上まとめると、スピン−スピン緩和時間 T2は横磁化が1/eに減少する時間である。ここまでの話では簡潔に話を進めるため、T2とT1の過程は分けて説明した。磁化ベクトルはZ軸方向に回復する前にXY平面を完全に埋め尽くしている。実際には、両方の過程はT2がT1よりも小さいか同じになるという条件の下に同時に進行する。横磁化の減衰に関しては2つの要因が影響する。
1)分子間相互作用による純粋なT2
2)Boの変動による磁場不均一による T2
これらの2つの要因の組合せが、実際の横磁化の減衰の原因となる。両者が合わさった時定数はT2スターと呼ばれ、T2*と表す。分子間相互作用によるT2と磁場不均一によるものとの関係は以下のように表される。
ラーモア周波数でZ軸の周りを回転する回転座標系では、ラーモア周波数の磁化ベクトルは
静止している。回転座標系では磁化MZの平衡状態へ回復は実験室系の場合と同様に見える。
回転座標系と同じ速度でZ軸の周りに回転する横磁化ベクトルは回転座標系では静止して見える。
回転座標系よりも速く進んでいる磁化ベクトルはZ軸の時計周りの方向に回転する。
回転座標系よりも遅く進んでいる磁化ベクトルはZ軸の反時計周りの方向に回転する。
ある試料中に、回転座標系に比べて速く回るものと遅く回るスピンパケットが混在している。試料の平均共鳴周波数が回転座標系の速度と同じ時には、MX'Y'のdephaseはこのアニメーションのようになる。
交流を流すと磁場の向きは交互に変化する。
交流の周波数に等しい周波数で回転する回転座標系では、X'方向の磁場は実験室系で直流を流した場合と同様に一定になる。
これは、ラーモア周波数で回転する回転座標系のまわりを同じ速度で運動するコイルと同じである。磁気共鳴では、コイルにラーモア周波数の交流を流して出来る磁場のことをB1磁場と呼ぶ。コイルを流れる交流をON，OFFすると、X'軸方向の B1磁場が作られる。
スピンがこのパルスに反応すると、与えられたB1磁場に軸のまわりに磁化ベクトルが回転する。回転する角度は磁場が印加されている時間
と磁場の大きさB1に依存する。
= 2
B1.
下記の例では、はT1, T2よりも十分短いと仮定している。
90oパルスはX'軸の時計回りに磁化ベクトルを90度回転させるパルスで、平衡磁化はY'軸上に倒れる。実験室系では、平衡磁化は螺旋状にZ軸からXY平面に倒れて行く。
なぜ、回転座標系がパルス磁場に対する磁化のふるまいを見るために役立つかがよくわかる。
180oパルスは、磁化ベクトルを180度回転させて平衡磁化を-Z軸に倒す。
どのような向きの磁化も回転方程式に従って運動する。例えばY'方向の磁化ベクトルはX'方向にB1磁場の180oパルスが印加されると-Y軸に倒れる。
X'とY'の間にある磁化ベクトルはX'方向にB1磁場の180oパルスが印加されるとX'とY'の間に倒れる。
回転の結果を求めるのには回転行列 (第2章の#2.6の座標変換を参照) を使う。はX'軸まわりの回転角を表す。 [X', Y',
Z] は回転前の位置ベクトル, [X", Y", Z"]
は回転後の位置ベクトルを表す。
ラーモア周波数で時間変動する磁場はスピン準位の遷移を引き起こし、その結果
MZを変化させる。次のアニメーションでは、水分子中の緑色の水素原子が，外部磁場
Boと青い水素原子が作る磁場の中で回転する様子を示している。緑色の水素原子の位置の磁場はsin関数になることに注目されたい。
分子の回転周波数にはバラツキがあり、ラーモア周波数に一致する部分だけがT1に影響する。ラーモア周波数は、Boに比例するから、T1は静磁場強度の関数として変化する。
一般には、T1はラーモア周波数で運動している分子の数に逆比例する。
周波数の分布は温度と液体の粘性に依存する。そのため T1は温度により変化する。 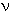oで示されたラーモア周波数はT1 (280 K ) < T1 (340 K)となる。人間の体温はT1に著しく変化を与えるような変動はしないが、粘性は組織によって大きく異なり、次のグラフに示されるように
T1に影響を与える。
変動する磁場はスピンのエネルギー準位を乱し、横磁化を減少させる。これは次のアニメーションの赤い水素原子が受ける
Boのプロットを見ると理解できる。ラーモア周波数と同じかそれ以下の分子の数はT1に反比例する。
一般に、緩和時間はBoが大きくなるにつれて増加する。これは、分子のランダムな運動の中で緩和に影響する周波数成分が少なくなるためである。